
Виктор Масалыгин
Тарту 2003
В наше время все большее развитие приобретает тенденция применения компьютера в обучении. Основными плюсами обучающих программ в сравнении их с печатными изданиями являются интерактивность и мультимедийность. Так, манипулируя устройствами ввода, пользователь может незамедлительно получать как визуальную, так и звуковую реакцию программы. Первой задачей разработчика оказывается все же нахождение адекватного визуального представления изучаемого материала, т.к. визуальный канал восприятия для большинства людей является главным, а наглядное представление некоей закономерности зачастую совпадает с ее пониманием. Совместное использование звука и изображения позволяет добавить наглядность к представлению знаний, относящихся к области звука, в частности к учению о музыкальной гармонии.
В данной работе делается попытка осветить проблему изучения музыкальной гармонии с использованием программного обеспечения, а также разработать программу, позволяющую заниматься музыкальной гармонией людям, не имеющим музыкального образования и не владеющим нотной грамотой.
В первой части работы кратко излагается необходимая основа предмета музыкальной гармонии, объясняются преимущества квинто-терцового представления нотного пространства. Основное внимание во второй части уделено исследованиям английского информатика Саймона Холлэнда (Simon Holland) в теории и преподавании музыки. Третья часть посвящена разработанной автором программе "Квинто-терцовая решетка": описаны возможности и интерфейс программы, приведены примеры ее применения.
В основе теории музыкальной гармонии лежит понятие консонанса – спокойного, ненапряженного, гармоничного созвучия тонов. К сожалению, гармонические связи между тонами не просматриваются явно ни на клавиатуре фортепиано, ни на нотном стане. Так, изучающий гармонию, видя смежными лишь мелодически близкие ноты, вынужден только подразумевать гармоническую связность музыкального пространства, нередко используя для этого специальную терминологию. Это делает учение о гармонии доступным лишь для музыкально образованных людей. В то же время, из-за его ясности и строгости, многие гармонические принципы могут быть понятны и ребенку, особенно при их наглядном изображении.
В 6 веке до н.э. Пифагор обнаружил, что в основе музыкального благозвучия лежат малые целочисленные отношения звуковых частот, соответствующие консонансам:
1:2 – октава,
2:3 – квинта,
3:4 – кварта,
4:5 – терция,
5:6 – малая терция.
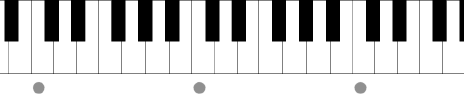
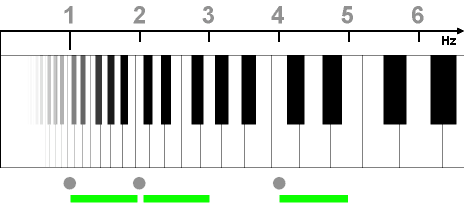
Связь между консонансами и малыми числовыми отношениями объясняет теория колебаний. Спектр музыкального звука кроме основной частоты содержит ряд кратных ей обертонов (гармоник). В числе первых из них – тоны, отличные от основного на интервалы: октава, квинта и терция (квинта и терция – по модулю октавы), что видно из рисунка 1b.
 a
a
 b
b
Рисунок 1. Особое значние октавы, квинты и терции.
Используемое в теории музыки понятие октавной эквивалентности связано с т.н. "феноменом октавы": звуки, отличающиеся на интервал кратный октаве (частоты отличны на степень двойки, рисунок 1a), имеют практически одинаковую гармоническую функцию. Это выделяет квинту и терцию, как главные, определяющие гармоническое значение, интервалы.
Об основополагающем значении квинто-терцовости в музыкальной теории говорят многие исследования в этой области.
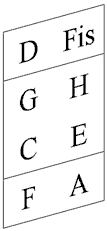
Тартуский музыкальный теоретик Яан Соонвальд берет за основу эти три консонанса для построения своей теории "благозвучной музыкальной системы" ("Звукоряды и созвучия благозвучной музыкальной системы в освещении графо-математического анализа", Тарту 1964). Он использует октавную эквивалентность и, выбрав начальный тон, сокращает отношения к нему частот остальных звуков до содержания лишь множетелей 3 и 5 (квинтовое и терцовое отношения). Основной идеей его работы является построение квинто-терцовых колонн, представляющих собой прямоугольный массив нот, содержащий квинты в одном направлении и терции в другом (рисунок 2).
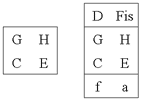
Рисунок 2. Колонны Соонвальда.
Колонна соответствует музыкальному звукоряду. Каждой колонне Соонвальд соотносит определенную константу вида 3n5k, указывающую, сколько квинт и терций в колонне. Соонвальд строит иерархическую систему колонн и подколонн, увеличивая колонны в терцовых и квинтовых направлениях, и вводит терминологию для обозначения колонн определенных размеров (констант) и созвучий определенных форм (15 – "осевой комплекс", 335 – "гармоническое звено", 3452 – "максимальное политональное звено", 3652 – "комбинированный звукоряд" и т.д.; рисунок 3).

Рисунок 3.
Следует заметить, что, не различая чистых октав, Соонвальд считает разными комматически отличающиеся звуки (совпадающие ступени лада, например D и d; рисунок 3 - справа), каждый имеет свое функциональное значение в колонне.
Наибольшую колонну – 3854 (45 звуков) – Соонвальд называет "звуковой областью" и утверждает, что она содержит все звуки любого произведения, написанного по т.н. "стройной теории".
Подход Соонвальда к функциональной значимости тонов в колонне (сведение гармонии к квинто-терцовости) может показаться излишне строгим, подобно теории Пифагора (конструктивным элементом которой кроме октавы была лишь квинта). Кажется, если нота "ре" иногда может иметь разные значения (D и d), то почему бы слушателю ни воспринимать ее в разных значениях одновременно – в этом случае ее положение в колонне не будет определено.
Юрий Холопов более гибко подходит к квинто-терцовости, освещая ее становление в историческом контексте.
Средневековая квинтовая структура диатоники (и распространенный в то время дорийский лад, в котором тоника имеет центральное положение и равноудалена от "краев" лада; рисунок 4 - слева) с осмыслением терцовых связей (прежде всего между тоникой и четвертой квинтой; рисунок 4 - справа) уступает место квинто-терцовости. Это сопровождается появлением новой основной единицы – трезвучия, и объясняет распространение эонийского и эолийского ладов (мажора и минора), где тоническое трезвучие оказывается центральным в квинтовой вертикали трезвучий S-T-D.
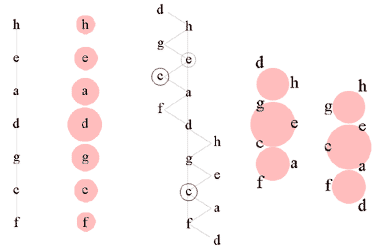
Рисунок 4. Осмысление терций, появление трезвучий.
Далее лад, расширяясь в квинтовом и терцовом направлениях, обретает все больше звуков, образуя квинто-терцовый массив – колонну Соонвальда (рисунок 5a).
 a
a 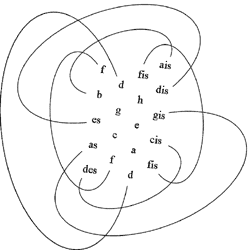 b
b
Рисунок 5. Замыкание "энгармонического шара".
Холопов отмечает более современную тенденцию "замыкания" лада на себя (как в квинтовом, так и в терцовом направлениях) и образования т.н. "энгармонического шара" (рисунок 5b). В нем функции созвучий определяются уже не только квинто-терцовыми отношениями: большую роль начинает играть симметричность нотного пространства (тритоновая, терцовые и секундовые симметрии). Как следствие этого – образование симметричных ладов.
Таким образом продолжается тенденция развития, переосмысления гармонической связности: от квинтовости (Пифагор, средневековье) к квинто-терцовости (западное многоголосье) и далее, к следующим системам организации – секундовым, тритоновым (в современной музыке). Квинто-терцовость, однако, до сих пор остается главным фактором гармонического родства звуков и созвучий.
Рынок программного обеспечения предлагают множество средств изучения музыкальной гармонии. В основном это программы, использующие общепринятую, нотную музыкальную запись. Кроме того, изучение гармонии зачастую предлагается в контексте определенного музыкального инструмента. Хочется, однако, определить взгляд на гармонию, как на основополагающий закон музыкальной организации, не имеющий ничего общего с нотной грамотой. С этой стороны, изучение гармонии может не прибегать ни к нотной записи, ни к особенностям какого-либо музыкального инструмента.
В связи с этим следует уделить внимание исследованиям английского информатика Саймона Холлэнда (Simon Holland), использующего в программном обеспечении по музыкальной гармонии квинто-терцовую решетку в качестве нотного пространства. Такой подход следует отнести к нестандартным методам изучения гармонии, однако, как будет показано ниже, весьма результативным во многих случаях.
Саймон Холлэнд расширяет применение квинто-терцовой решетки для обучения музыкальной гармонии. Он проектирует компьютерную программу, которая изображает квинто-терцовую решетку, реагирующую на щелчки мыши и соединенную со звуковым устройством вывода (MIDI секвенсором). Получившийся "музыкальный инструмент", интерактивное средство манипуляции, призвано облегчить экспериментирование и анализ гармонии в первую очередь для новичков, не обладающих музыкальным образованием, но также и для опытных музыкантов.
В статьях “New cognitive theories of harmony applied to direct manipulation tools for novices” (1987) и “Learning about harmony with Harmony Space: an overview” (1994) Холлэнд описывает свойства квинто-терцовой решетки (Harmony Space), возможности и интерфейс своей программы, а также некоторые примеры применения и проведенные им эксперименты.
Холлэнд основывает свою работу на двух современных исследованиях в области восприятия музыки: работах Кристофера Лонге-Хиггинса (Chrisopher Longuet-Higgins, 1962) и Геральда Бальцано (Gerald Balzano, 1980). Как и система Яана Соонвальда, теория Лонге-Хиггинса исходит из ключевой роли интервалов, чьи частотные соотношения выразимы как произведения трех коэффициентов: 2, 3 и 5. Теория Бальцано использует алгебраическую теорию групп и сравнивает 12 музыкальных тонов с циклической группой C12, что имеет большую аналогию с "энгармоническим шаром" Юрия Холопова. Теории приводят к представлению нот двумерным массивом, что позволяет "расщепить" хроматический ряд на два направления в плоскости, и дает возможность придать конкретную форму гармоническим структурам и отношениям в гармоническом пространстве.
Прежде всего, все ноты диатонического звукоряда оказываются заключенными в компактный регион (область ключа). Слева на рисунке 6 – ступени диатонического звукоряда (обозначены римскими цифрами) в области ключа. Трезвучия также представляют собой компактные объединения. Доминантовое (D) и субдоминантовое (S) трезвучия максимально близки к тоническому (T), образуя вертикаль S-T-D. Из рисунка 6 видно, что три главных трезвучия содержат все 7 нот диатонической гаммы, и тоническое трезвучие – буквально центрально. Также семь нот оказываются на одной вертикальной линии (рисунок 6 - вправа), что иллюстрирует квинтовую структуру диатоники.
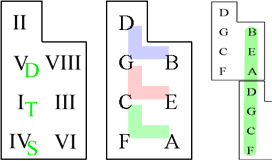
Рисунок 6. Область ключа.
Движение области ключа по вертикали вверх или вниз соответствует модуляции в доминанту или субдоминанту.
Стоит упомянуть об интересном сравнении Холлэнда: преобладающие в западной тональной гармонии движения вниз на квинту он метафорически сравнивает с гравитацией. Так, главная гармоническая каденция TSDT является сначала "падением" из T в S, затем малым мелодическим сдвигом (лишь на 2 полутона) в противоположную по вертикали от T сторону, и, наконец, естественным возвращением в T.
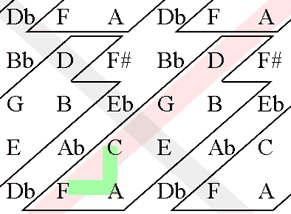
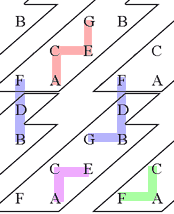
В своей программе Холлэнд направляет квинтовые связи по диагонали (вправо вверх), для того, чтобы терции (малая и большая), составляющие большинство аккордов получили более сравнимые направления: вертикаль и горизонталь. Также это позволяет выделить хроматический ряд как другую диагональ (вправо вниз), для того чтобы мелодические связи тоже приобрели наглядность. Таким образом, "гармоническое пространство" совмещает хроматический и квинтовый ряды (рисунок 7a). Из рисунка 7b видно, что аккорды терцовой структуры обретают естественную и выразительную форму в пространстве. На рисунке 8 вид одной из версий программы Холлэнда.
 a
a
 b
b
Рисунок 7.
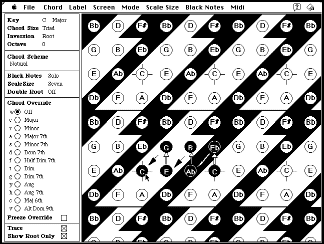
Рисунок 8. Одна из версий программы Холлэнда.
Главными возможностями программы
Холлэнда являются:
* манипулирование областью ключа и
* режим аккорда, когда один щелчок мыши приводит к
воспроизведению нескольких нот.
Клавиши курсора непосредственно управляют областью ключа, позволяя осуществлять модуляцию (иными словами, двигать область ключа) на разные интервалы вверх и вниз.
Режим аккорда позволяет проигрывать аккорд терцовой структуры, с основным тоном в выбранной ноте и вписывающийся в область ключа. Также есть возможность проигрывания стандартных аккордов вне зависимости от области ключа.
С одной из ранних версий своей программы Холлэнд провел эксперимент. Для этого были выбраны 5 человек (в возрасте от 8 до 37 лет), не обучавшихся ранее музыке и не имеющих явных музыкальных способностей. С каждым Холлэнд провел индивидуальный сеанс с использованием своей программы, выступая в роли инструктора. Время (от 30 минут до 2,5 часов) и диапазон задач (от простого аккомпанемента до композиционных упражнений) определялись персонально.
Результаты эксперимента оказались следующими. Все пользователи быстро уяснили основы интерфейса программы. Большинство за несколько минут смогли играть аккомпанемент к отрывкам в разных тональностях, используя стандартные аккорды. Некоторые пользователи оказались в состоянии играть более сложные гармонические последовательности, в том числе использующие модуляцию.
Холлэнд использовал в эксперименте композицию Джона Колтрэйна "Гигантские шаги" (John Coltrane, "Giant Steps"), в которой применяется периодическая модуляция вниз на большую терцию, ее траектория изображена на рисунке 8. Выяснилось, что благодаря наглядности квинто-терцового пространства, необычная (но, по сути, простая) гармоническая траектория отрывка была быстро распознана некоторыми пользователями. Это иллюстрирует возможности комплексного (геометрически-музыкального) подхода к гармонии. Так, например, пользователь может видеть различные направления модуляции, сопоставляя их со слышимым преобразованием.
Исследования Саймона Холлэнда позволяют сделать вывод о плодотворности и перспективности использования квинто-терцовой решетки в учебном программном обеспечении в области музыкальной гармонии. Очевидно, что особенные преимущества подход имеет для людей с повышенной значимостью визуального канала восприятия.
Интернет позволяет найти упоминания о других программах, подобно программе Холлэнда использующих квинто-терцовое представление нотного пространства.
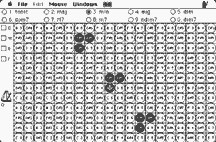
На рисунке 9а экран программы Harmony Grid (Levitt, D. H. and Joffe, E.), написанной в 1986 году для Apple Macintosh, внешне похожей на программу Холлэнда, однако не использующей изображения области ключа.
На рисунке 9b пример "гармонического пространства", реализованного на основе исследований Саймона Холлэнда в среде MusES).
 a
a 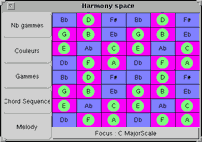 b
b
Рисунок 9.
Автору не удалось найти упоминания о программе подобного рода, написанной для MS Windows. Это явилось главным основанием для разработки программы "Квинто-терцовая решетка". Также причиной послужили соображения, касающиеся вида и возможностей программы. Программа "Квинто-терцовая решетка" изображена на рисунке 10.
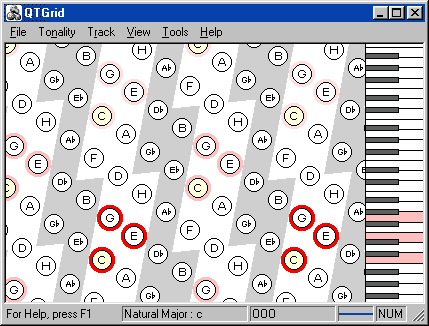
Рисунок 10. Программа "Квинто-терцовая решетка".
Программа "Квинто-терцовая решетка" использует квинто-терцовое представление нотного пространства и предназначена для изучения музыкальной гармонии, экспериментирования в области теории и анализа гармонии. Программа может быть полезной как для пользователей, не имеющих музыкального образования (в частности, не владеющих нотной грамотой), так и для профессионалов.
Программа написана в среде MS Visual C++ 6.0 для операционной системы MS Windows. Приложение и руководство пользователя, а также файлы примеров, демонстрирующих некоторые возможности программы, доступны по адресу http://bntr.planet.ee/hot/Program.html#QTGrid.
Основными возможностями программы
являются:
* управление областью ключа мышью и цифровой
клавиатурой,
* режим аккорда,
* запись, сохранение и загрузка нотной
последовательности (формат Midi),
* режим карандаша, сохранение и загрузка
изображения (формат Bmp).
Вид программы
Главным внешним отличием от других, приведенных выше, программ, использующих квинто-терцовое представление, является вид квинто-терцовой решетки, изображенной на главном окне программы (рисунок 10). Ноты равной высоты расположены на одной горизонтали. Одноименные ноты (отличающиеся на кратный октаве интервал) принимают вид прямой ромбовидной сетки, что придает решетке вид обоев.
На рисунке 11a показано, что квинтовое отношение соответствуют вертикальному (чуть вправо) направлению, терцовое – диагональному (вправо вверх). Интервал другой диагонали соответствует малой терции. Горизонтально (чуть вверх) направлен хроматический (полутоновый) ряд. Его равномерное возрастание позволяет спроецировать все ноты на правую сторону, где размещена клавиатура фортепиано. В таком виде вертикальное и горизонтальное направления на решетке соответствуют гармоническим и мелодическим музыкальным связям. Ноты на сером фоне соответствуют не содержащимся в области ключа. Основной тон тональности выделен желтым.
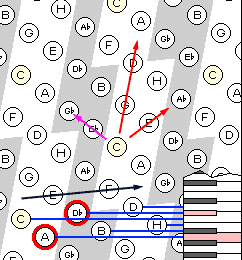 a
a
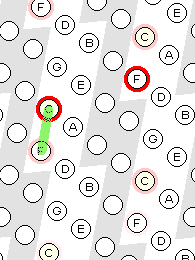 b
b
Рисунок 11.
На рисунке 11b показано, как высвечивание воспроизводящихся нот сопровождается своеобразным "эхом" (менее ярким высвечиванием) в ближайших октавах, что иллюстрирует октавную эквивалентность и позволяет видеть гармоничность обращенных интервалов, например кварты (кварта = октава - квинта).
Управление мышью
Нажатие левой кнопки мыши (также клавиши клавиатуры) вызывает звучание ноты. Правая кнопка мыши служит для управления областью ключа: щелчок на ноте делает ее основным тоном новой тональности, что соответствует модуляции.
В программе предусмотрен режим карандаша, позволяющий на виде решетки левой кнопки мыши оставлять полупрозрачный след выбранной толщины и цвета. Нарисованное изображение может быть сохранено и загружено.
Управление клавиатурой
Клавиатура выступает устройством ввода нот с двух режимах: квинто-терцовой решетки (рисунок 12a) и фортепианной клавиатуры (рисунок 12b).
 a
a
 b
b
Рисунок 12. Два режима управления клавиатурой.
Режим аккорда
В режиме аккорда программа позволяет при выборе одной ноты проигрывать одновременно несколько (аккорд). Структура аккорда задается цифровыми клавишами основной клавиатуры.
Основной функцией режима является проигрывание аккорда терцовой структуры, вписывающегося в область ключа и с основным тоном в выбранной ноте. Пользователь указывает количество терций в аккорде (интервал, трезвучие, септаккорд и т.д.), пропущенные тоны в неполном аккорде. Есть возможность установить в основе аккорда вне зависимости от области ключа соответственно минорное, мажорное трезвучие либо минорный или мажорный септаккорд. Вращение колеса мыши обращает аккорд (повышает его нижние звуки на октаву).
Дополнительные окна
С помощью окна лада (рисунок 13a) можно установить текущим любой лад.
Окно оркестра (рисунок 13b) позволяет сформировать оркестр из инструментов General Midi и выбирать один из них текущим. Звук каждого инструмента отображается на квинто-терцовой решетке своим цветом.
 a
a
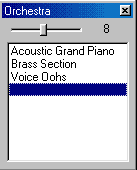 b
b
Рисунок 13. Дополнительные окна.
Более подробно интерфейс и возможности программы описаны в приложенном руководстве пользователя.
Квинто-терцовая решетка, изображенная
на главном окне программы, имеет универсальный
для теории музыки характер, сочетая в себе многие
свойства, полезные для представления
гармонических закономерностей:
* иллюстрирует квинтовые и терцовые
гармонические связи, являющиеся основным
фактором гармонической организации,
* не утрачивает при этом изображения полутоновой
связи,
* совмещает квинтовый, хроматический и
диатонический ряды,
* придает естественную форму гармоническим
структурам,
* иллюстрирует симметричное строение нотного
пространства, обнаруживая тенденцию
возникновения симметричных ладов,
* дает альтернативный взгляд на музыкальную
гармонию.
Кроме изучения теории музыкальной гармонии (а также обучения) наглядные возможности программы могут найти применение при анализе музыкальных отрывков, экспериментировании с гармоническими последовательностями, композиции. Также программа может быть использована как музыкальный инструмент или своеобразный Midi-проигрыватель.
Ниже приведены примеры, демонстрирующие наглядные возможности программы.
Аналогия тяготения гармонической траектории с гравитацией хорошо видна на примере прелюдии И. С. Баха C-dur (рисунок 14). Легко поняв основной принцип стремления вниз, пользователь может подражать элементам гармонии Баха.

Рисунок 14. Прелюдия C-dur И. С. Баха.
На рисунке 15 пример наглядной траектории джазовой гармонии из композиции Джона Колтрэйна "Гиганские шаги", демонстрирующей кроме движения вниз колебания в терцовом направлении.
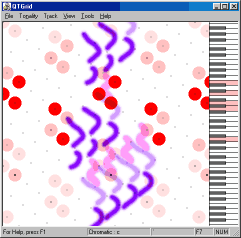
Рисунок 15. "Гиганские шаги" Джона Колтрэйна.
Квинто-терцовая решетка дает возможность легко свести некоторые нестандартные аккорды к квинто-терцовости (гармонически связать), что может быть полезным для определения гармонической функции. Например, видно, что в аккорде f-b-d-e тон e связан с трезвучием b-d-f через g, а также через a (рисунок 16 - слева). В однотерцовом отношении (начатом осваиваться в XIX веке) также видна связь с тоникой: справа на рисунке 16 указаны терцовое и квинтовое направления, связывающие трезвучия c-e-g и c#-e-g#.
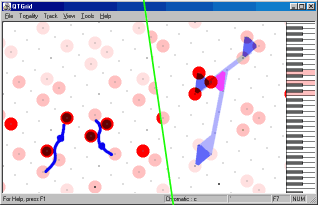
Рисунок 16. Гармоническая связываемость.
Равномерность квинто-терцовой решетки может быть использована и для демонстрации структур атональной музыки, свойственной XX веку. Например, хорошо видна изящность, законченность и симметрия серии из "Скрипичного квартета" Антона Веберна (опус 28) b-a-c-h – d#-e-c#-d – f#-f-g#-g (рисунок 17).
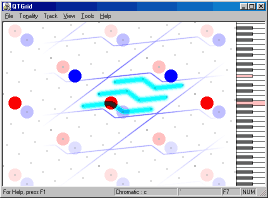
Рисунок 17. "Скрипичный квартет" Антона Веберна.
В работе сделана попытка разработки удобного средства для MS Windows для экспериментирования с музыкальной гармонией. Для этого разобраны основные законы гармонической организации, приведены примеры существующих программных средств, сделан вывод о преимуществе квинто-терцового представления нотного пространства. За основу программы взята работа Саймона Холлэнда.
Исходя из приведенных примеров, демонстрирующих наглядные возможности программы, кажется очевидным, что написанная программа значительно упрощает понимание закономерностей гармонии и экспериментирование с гармоническими последовательностями.
Однако по поводу перспектив применения программы следует упомянуть следующее. На прошедшей 3 мая 2003 года в Тарту конференции "Eesti Muusikateaduse Seltsi Tartu paev"1 доклад автора "Kvintide ja tertside vorgustik kui harmoonia-alase oppetarkvara loomise alus"2 (в котором были описаны проблемы, затронутые в данной работе, и продемонстрированы основные возможности написанной программы) не вызвал отклика у присутствовавших преподавателей гармонии. Тартуский композитор и преподаватель гармонии Март Яансон объяснил незаинтересованность учителей непривычностью подхода, использования компьютера в преподавании музыки. Это подсказывает, что применение программы, скорее всего, ограничится узким кругом заинтересованных лиц.
Хочется надеяться, что через некоторое время ситуация изменится, применение компьютера в музыкальных учебных учреждениях станет более распространенным и обнаружится заинтересованность и в нестандартных методах обучения. Это сможет стимулировать дальнейшую разработку данного программного обеспечения.
1 "Тартуский день Эстонского Общества
Музыкознания"
2 "Квинто-терцовая решетка как основа
создания учебного программного обеспечения в
области гармонии"
Автор благодарит Яана Росса за поддержку в работе над теоретической частью, помощь в подготовке доклада. Лишь благодаря своевременному совету Марта Яансона об участии в конференции, автору удалось узнать отношение к работе многих учителей гармонии Эстонии. Без хладнокровного терпения Юри Кихо в руководстве разработкой программы она не могла быть создана. Также автор благодарит Анне Виллемс за объективную критику во время защиты работы
Соонвальд, Я. Звукоряды и созвучия благозвучной музыкальной системы в освещении графо-математического анализа. Тарту 1964.
Холопов, Ю. Гармония: теоретический курс. Москва "Музыка" 1988.
Holland, S. New cognitive theories of harmony applied to direct manipulation tools for novices. 1987 (http://mcs.open.ac.uk/sh2/).
Holland, S. Learning about harmony with Harmony Space: an overview. 1994 (http://mcs.open.ac.uk/sh2/).