Viktor Massalõgin
Antud ettekanne oli valmistatud Jaan Rossi juhendamisel ning esitatud "Eesti Muusikateaduse Seltsi Tartu paev" konverentsil 3. mail 2003.
Tänapäeval on arvutit hakatud õppetöös üha enam ja enam kasutama. Arvutiprogrammide eelis kirjalike õppematerjalidega võrreldes seisneb esiteks nende interaktiivses iseloomus ja teiseks multimeedia vahendite kasutamises. Teiste sõnadega, kasutaja saab tavapäraste sisestusvahendite nagu hiir või klaviatuur abil esile kutsuda programmvarustuse reaktsioone kas siis visuaalsel kujul arvuti kuvaril või helilisel kujul. Programmeerija kõige esmaseks ülesandeks on siiski lahendada tulevale ülesandele visuaalse ekvivalendi loomine, kuivõrd inimene saab absoluutse enamuse informatsiooni teda ümbritsevast keskkonnast kätte nägemise vahendusel.
Harmoonia teooria aluseks muusikas on õpetus konsonantsidest ja dissonantsidest. Tuleb märkida, et muusikalise harmoonia elemendid ja nende ühendamise seaduspärasused ei ole õpilase jaoks vahetult jälgitavad ei klaveri klaviatuuril ega ka noodikirjas. Kui rääkida helide vahelistest meloodilistest seostest, siis - erinevalt harmoonilistest seostest - on nad klaviatuuril selgesti viisualiseeritud. Harmooniline sugulus helide vahel jääb aga õpilase jaoks märksa abstraktsema iseloomuga kategooriaks, millest arusaamiseks lisaks kõigele muule on tarvis tunda spetsiaalset terminoloogiat. Seetõttu eeldab harmoonia teooriast arusaamine õpilaselt teatud tasemel muusikalist haritust. Teiselt poolt peab aga märkima, et paljud harmoonia teooria põhimõtted on oma selgusest ja rangusest tingituna põhimõtteliselt arusaadavad isegi lapsele, eriti kui neid piisava näitlikkusega esitada.
Kvintide ja tertside võrgustiku kasutamine võib anda didaktiliselt positiivseid tulemusi, sest kvint ja terts on intervallid, mis loovad aluse harmoonilise muusikalise materjali organisatsioonile.
Selles ettekandes kavatsen rääkida oma informaatika-alasest diplomitööst. Töös olen loonud arvutile programmvarustuse, mille ülesandeks on muusikalise harmoonia süsteemi viisualiseerimine kvintide ja tertside võrgustikule tuginedes. Muusikateooria osas tugineb diplomitöö Moskva konservatooriumi professori Juri Holopovi õpikule "Teoreetiline harmooniakursus", arvutiteaduse osas aga inglise informaatiku Simon Hollandi töödele. Käesoleva töö ajendiks on olnud Euroopa kultuurile iseloomulik püüe seletada esteetiliselt ilusat objektiivsetest alustest lähtudes ehk, nagu vene keeles öeldakse - "поверить гармонию алгеброй".
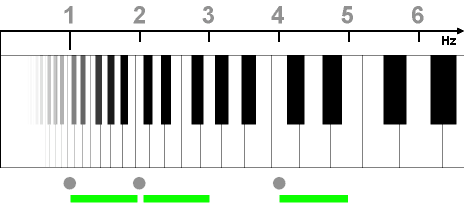
Iga kindla kõrgusega heli spekter sisaldab lisaks põhitoonile veel ka ülemhelisid, mille sagedused on põhitooni kordsed. ülemhelide rea alumiste liikmete vahel tekivadki konsonantsed intervallid.

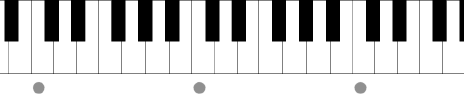
ülemhelide rida nimetatakse ka naturaalseks helireaks ning see moodustab harmooniliste suhete aluse muusikas. Peamisteks konstruktiivseteks intervallideks muusikalise harmoonia vallas on oktav, kvint ja terts.
Tartus tegutsenud matemaatik ja muusikateoreetik Jaan Soonvald ongi oma kandidaadiväitekirjas "Звукоряды и созвучия благозвучной музыкальной системы" "heakõlalise helisüsteemi" aluseks võtnud eelpoolnimetatud kolm intervalli. Oktavi ekvivalentsi põhimõtet kasutades ehitab ta valitud lähtehelist kõik teised helid üles kordajaid 3 ja 5 kasutades, mis vastavad kvindile ja tertsile. Soonvaldi töö peamiseks ideeks on kvindilis-tertsilise helide maatriksi moodustamine, mille elemendid oleksid ühes suunas (vertikaalis) paigutatud kvindi vahekorrast lähtudes ning teises suunas (horisontaalis) tertsi vahekorrast lähtudes. üks maatriksi segment (tulp) vastab muusikalisele helireale. Iga tulbaga seab Soonvald vastavusse konstandi 3n5k, mis vastab kvintide ja tertside hulgale tulbas.
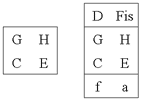
Soonvaldi töös kujuneb tulpade ja alamtulpade vahel välja hierarhiline süsteem, mis -laieneb nii tertside kui ka kvintide suunas. Ta arendab välja terminoloogia tähistamaks erineva suurusega j tulpasid a erinevaid muusikalisi kooskõlasid, mis vastavad erinevatele konstantidele. (15 - telgkompleks, 335 - harmooniline tuum, 3452 - maksimaalne polütonaalne tuum, 3652 - kombineeritud helirida jne.)

Oluline on märkida, et kuigi Soonvald oktavite vahel vahet ei tee, eristab ta siiski komma võrra üksteisest erinevaid helisid, näiteks helirea kattuvaid elemente D ja d, millest igaühel on tulbas erinev funktsionaalne tähendus.
Kõige suuremat tulpa, mis koosneb 45 helist, nimetab Soonvald helide vallaks ning väidab, et see peab sisaldama mistahes heliteose kõik helid, juhul kui see heliteos on loodud reeglipärase helisüsteemi alusel.
Soonvaldi lähenemisviis helide funktsionaalsele asendile tulbas ehk, teiste sõnadega, harmoonia taandamine Soonvaldi poolt kvindilis-tertsilistele suhetele, võiks tunduda üleliia dogmaatilisena, nii nagu seda on ka Pythagorase süsteem, mis konstruktiivse elemendina lisaks oktavile tunnistab vaid kvinti. Kui näiteks re-noodile võivad tabelis vastata nii D kui ka d, siis miks ei võiks kuulaja neid erinevaid re vorme tajuda samasugustena, nii et re asukoht tabelis poleks ilmtingimata fikseeritud?
Juri Holopovi lähenemisviis kvindilis-tertsilistele suhetele on Soonvaldiga võrreldes paindlikum. Holopovi käsitlust iseloomustab ennekõike)selle ajalooline iseloom. Diatoonilise süsteemi puht-kvindiline struktuur keskajal ning koos sellega dooria helilaad, milles toonikal on keskne tähendus, kuivõrd ta asetseb laadi "servadest" võrdsel kaugusel, loovutab tasapisi oma koha kvindilis-tertsilistele suhetele, sedamööda kuidas areneb arusaamine tertsilistest suhetest (eelkõige toonika ja arvuliselt neljanda kvindi järel oleva heli vahel) ja neid osatakse hakata lahti mõtestama. Koos sellega tekib süsteemis uus keskne element - kolmkõla ning laadide seas hakatakse eelistama jooniat ja eooliat ehk mažoori ja minoori. Neis laadides on toonika kolmkõla S-T-D kvintide järgnevuses kesksel positsioonil.
Edasi laieneb laad nii kvintide kui ka tertside suunas ja haarab endasse üha rohkem ja rohkem helisid, kuni tekibki kvintidest ja tertsidest koosnev maatriks ehk Soonvaldi tulp.
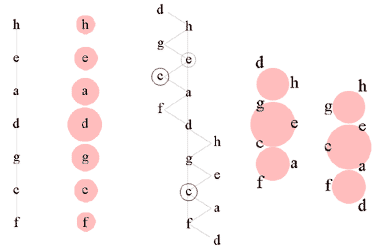
Holopov analüüsib ka kvintide ja tertside massiivis hilisemal ajal aset leidnud protsesse nagu laadi "sulgumine" endasse (mis võib toimuda nii kvintide kui ka tertside suunas) või nn enharmoonilise kera moodustumist. Selles keras ei määra kooskõlade funktsionaalsust enam kvindilis-tertsilised suhted, vaid pigem sümmeetria printsiip helisüsteemis. Sümmeetria võib esineda eri suurusega intervallide - tritoonide, tertside või sekundite - tasandil. Niimoodi tekivad sümmeetrilised laadid.
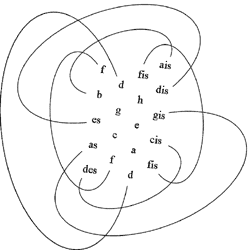
Niisiis võib helisüsteemi arengus tähendada üldisemat tendentsi, mille käigus harmooniliste sidemete iseloom tasapisi muutub. Kvindilise suguluse (Pythagoras, keskaeg) vahetab välja kvindilis-tertsiline sugulus (mitmehäälsus Lääne muusikas) ning selle omakorda sekundilised ja tritoonilised suhted (XX saj muusika). Sellele vaatamata on kvindilis-tertsilised suhted tänapäevani säilitanud erilise koha helide ja nende komplekside vahelise harmoonilise suguluse määratlemisel.
Siirdugem nüüd Simon Hollandi tööde juurde, kelle eesmärgiks on rakendada kvintide ja tertside võrgustikku muusika didaktikas, täpsemalt - harmooniakursuse õpetamisel. Holland on arvutile kirjutanud programmi, mis kujutab arvuti ekraanil kvintide ja tertside võrgustikku. Ta eeldab, et arvutil on olemas MIDI-liides. Selle tulemusel kujuneb arvutist omamoodi muusikainstrument, interaktiivsete omadustega tööjaam, mille abil saab harmoonia teooria vallas hakata korraldama eksperimente ja tegelema harmoonia analüüsiga. Arvestades seda, et tänapäeva noorsoo hulgas on oskus arvutiga töötada üldiselt levinud, sobib Simoni Hollandi leiutis kasutamiseks ka nendele inimestele, kelle süstemaatiline haridus muusikateooria vallas on napp või siis puudub hoopis. Selle kõrval võib Hollandi loodud programmvarustus huvi pakkuda ka professionaalidele.
Nendes artiklites kirjeldab Holland kvintide ja tertside võrgustiku, mida ta tähistab inglisekeelse sõnaga "harmony space", aga ka loodud arvutiprogrammi ja kasutajaliidese omadusi. Holland esitab ka näiteid selle kohta, kuidas programmi kasutada, ning kirjeldab programmi abil sooritatud eksperimente.
Hollandi töö teoreetiline osa tugineb paljuski muusikapsühholoogide Chrisopher Longuet-Higginsi (1962) ja Gerald Balzano (1980) töödele. Nagu Soonvaldi, nii lähtub ka Longuet-Higginsi teooria selliste muusikaliste intervallide võtmerollist helisüsteemis, mille koostis-helide sagedussuhted on väljendatavad arvude 2, 3 ja 5 korrutise kujul. Balzano teooria lähtepunktiks on algebraline rühmateooria. Ta võrdleb oktavis sisalduvat 12 muusikaheli tsüklilise rühmaga C12, millel on suurem analoogia Holopovi enharmoonilise keraga. Kumbki teooria päädib muusikalise helisüsteemi kahemõõtmelise kujutisega, mis võimaldab kromaatilise helirea tasapinnal horisontaali ja vertikaali kasutades kahemõõtmeliselt lõhestada. Nii omandavad harmoonilised struktuurid õpilase jaoks arvuti ekraanil märksa konkreetsema iseloomu kui muidu.
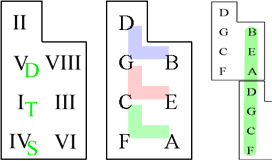
Hollandi programmis on kvindilised suhted paigutatud diagonaalselt, horisontaalis ja vertikaalis jooksevad aga vastavalt suured ja väikesed tertsid. Selle tulemusel kujutab maatriksi teine diagonaal kromaatilist helirida, mis muudab lisaks harmoonilistele ka meloodilised seosed helide vahel märksa kujukamaks. Nii ühendab Holland kahemõõtmelises harmoonilises ruumis teineteisega kvindiringi ja kromaatilise helirea kujutise.
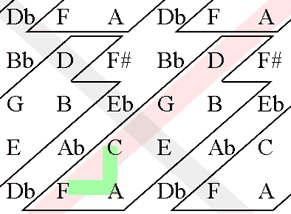
Tertside alusel üles ehitatud mažoorsed ja minoorsed kolmkõlad, sept- ja noonakordid omandavad ruumis loomuliku ja väljendusrikka kuju.
Holland märgib, et tema programmist on olemas realisatsioonid Apple MacIntoshi ja Unixi keskkonna jaoks, kuid leida neid pole mul õnnestunud, võin ainult näidata, kuidas programm välja näeb.
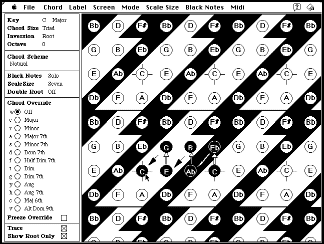
Olen Hollandi idee realiseerinud Eestis levinud MS Windows keskkonnas. Minu programm lähtub põhimõtteliselt Hollandi artiklites väljendatud ideedest, kuigi täies ulatuses ta nendega ei kattu.
Minu programmis on helisüsteemi graafilise esituse kuju omakorda veidi teisendatud. Oktavid kujutavad siin enesest rombikujulist võrgustikku. Nad asetsevad üksteise kohal. See võimaldab paigutada kromaatilise helirea püsttelge pidi ühtlaste vahedega ja projitseerida selle tasapinna paremasse serva, kuhu olen paigutanud klaviatuuri. Sellisel kombel kujutatuna vastavad vertikaal ja horisontaal harmoonilistele ja meloodilistele sidemetele helisüsteemis.
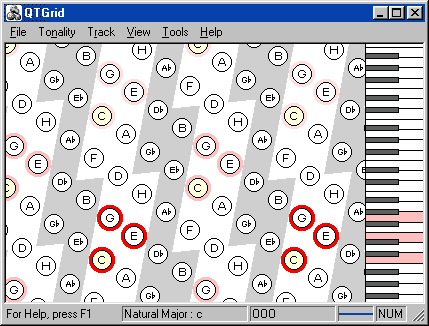
Kui programmis pöörduda mingi noodi poole, siis kaasneb sellega automaatselt, nagu omamoodi kaja, teiste tema suhtes oktavi vahekorras olevate, nootide läbivalgustamine. See võte muudab õpilase jaoks näitlikumaks oktavi ekvivalentsi mõiste ning lubab paremini aru saada intervallide pöörete kohast helisüsteemis (nt kvart kui kvindi pööre).
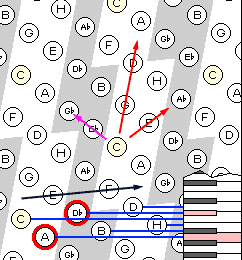
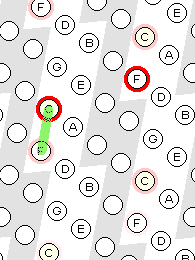
Programmi poolt pakutavate võimaluste seas peamised on: manipulatsioonid helistikuga ja töö akordi režiimis, kus ühe klahvile-vajutuse või hiireklõpsuga aktiveeritakse korraga mitu nooti.


Kursori klahvide abil saab vahetult juhtida helistiku ala ning mooduleerida kvindi (või mõne muu intervalli) võrra, kõrgemal või madalamal asuvasse helistikku. Toonika on alati tähistatud kollase värviga. Toonika asukohta on võimalik muuta, säilitades sealjuures helistiku asukoha võrgustikus, ja vastupidi. Nii saame jälgida diatooniliste laadide gradatsiooni (lüüdia, joonia,.. lokria). Laadi aken võimaldab defineerida mistahes laadi mistahes astmelt.

Akordi režiimis on võimalik esitada tertsilise struktuuriga akorde, mille põhitoon vastab valitud klahvile ja mis püsib helistiku ala piirides. Numbreid tähistavate klahvide abil saab kindlaks määrata tertside hulga akordis (intervall, kolmkõla, septakord jne), samuti osutada puuduvatele akordihelidele mittetäielikes akordides. Samuti on olemas võimalus mängida standardseid akorde helistiku alast sõltumatult.
Tasub meenutada veel üht huvitavat võrdlust Hollandil, mis tugineb harmooniliste seoste vertikaalsele iseloomule. Nimelt on Lääne tonaalsele muusikale väga iseloomulik V-I järgnevus, kus bass liigub kvindi võrra alla. Holland kõrvutab sellist järgnevust metafooriliselt Maa külgetõmbejõuga. Sel moel toimub TSDT kadentsis alguses "langemine" subdominanti, seejärel väikse meloodilise intervalliga liikumine toonika suhtes vastupidises suunas ning lõpuks loomulik tagasipöördumine toonikasse.
Järgmisena tahaksin Bachi Preluudi C-duur näitel osutada sarnasusele gravitatsioonijõu toimega.

Holland on oma programmi algset versiooni kasutades sooritanud järgmise eksperimendi. Ta kasutas selles katses inimesi, kes muusikat polnud varem õppinud, ning kes polnud muusikaliselt ka kuigi võimekad. Holland tegeles nendega, olles ise õpetaja rollis. Katsealustele antud ülesanded võisid olla isikuti erinevad (lihtsa saatepartii esitamisest kuni keeruliste kompositsiooni-tehniliste ülesannete lahendamiseni).
Katse tulemused olid järgmised. Kõik osavõtjad õppisid programmi kiiresti kasutama. Enamik inimesi omandas mõnede minutite jooksul oskuse programmi abil erinevates helistikes meloodiat saata, kasutades selleks standardseid akorde. Mõned kasutajad õppisid kasutama ka keerulisemaid akordijärgnevusi, sealhulgas selliseid, mis sisaldasid modulatsioone.
üheks Hollandi poolt toodud näiteks on John Coltrane'i pala Giant Steps, kus kasutatakse perioodiliselt moduleerimist suure tertsi võrra allpool asuvasse helistikku.
Selgus, et kvintide ja tertside võrgustiku näitlike omaduste tõttu, suutsid kasutajad kirjeldatud muusikalõigu ebatavalisest, kuigi oma olemuselt lihtsast, harmoonilisest trajektoorist küllaltki kiiresti aru saada. Selle näite abil võib aru saada kompleksse geomeetrilis-muusikalise lähenemise eelistest, harmoonia teooria seisukohast. Kasutaja võib näiteks jälgida erisuunalisi modulatsioone ning seostada neid oma kuuldeliste ettekujutustega.
Nüüd näete, kuidas Coltrane'i palast "Giant steps" pärit harmooniline järgnevus võrgustikul liigub.
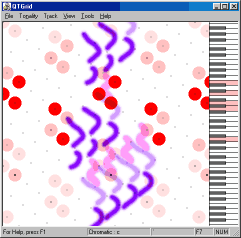
Lubage mul järgnevalt nimetada veel mõned võimalused kvintide ja tertside võrgustiku kasutamiseks.
Kvintide ja tertside võrgustiku abil saab ilma vaevata näha mõnede mittestandardseteks peetavate akordide kvindilis-tertsilist iseloomu, mis muudab nende määramise kergemaks. Näiteks akordis f-b-d-e on heli e kolmkõlaga b-d-f seotud nii g kui ka a kaudu.
Seos toonikaga on võrgustiku abil ilmne ka nn samatertsilistes akordides, mida hakatakse kasutama alates 19. sajandi algusest. Nt akordid c-e-g ja cis-e-gis on teineteisega seotud toonikast tertside suunas (c-e-gis-c) ja kvintide suunas (e-h-fis-cis-gis) liikumise kaudu.
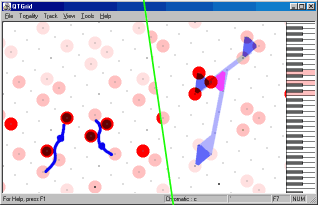
Kvintide ja tertside võrgustiku võrdmõõtmelisust saab kasutada ka atonaalses muusikas kasutatavate struktuuride demonstreerimiseks. Anton Weberni teoses op 28 kasutatud seeria elegantsus, lõpetatus ja sümmeetria on võrgustikul ilmne. (b-a-c-h - dis-e-cis-d - fis-f-gis-g).
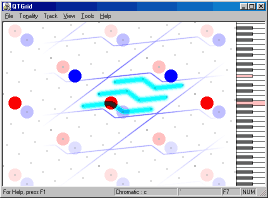
Usun, et kogemustega ja motiveeritud muusik suudab ilma pingutusteta leida kvintide ja tertside võrgustikule ka teisi tarvitusviise kui need, mida mul oli eespool võimalik demonstreerida. Kvintide ja tertside võrgustikul on harmoonia teooria seisukohast universaalne iseloom. Tema abil saab:
Lõpuks tahaksin nimetada, et programmi praegune versioon pole lõplik: seda saab vajaduse korral täiendada.
Programmi asukoht: http://bntr.planet.ee/wiki/?id=qtgrid
Соонвальд, Я. Звукоряды и созвучия благозвучной музыкальной системы в освещении графо-математического анализа. Тарту 1964.
Холопов, Ю. Гармония: теоретический курс. Москва "Музыка" 1988.
Holland, S. New cognitive theories of harmony applied to direct manipulation tools for novices. 1987.